You and your friend work out how much you should get back after you lend them ₹10,000 a year later. But here’s the catch: you get various answers. One of you utilized simple interest, whereas the other employed compound interest. That little adjustment in how you do things can make your money grow in a different way, perhaps by thousands of rupees over time.
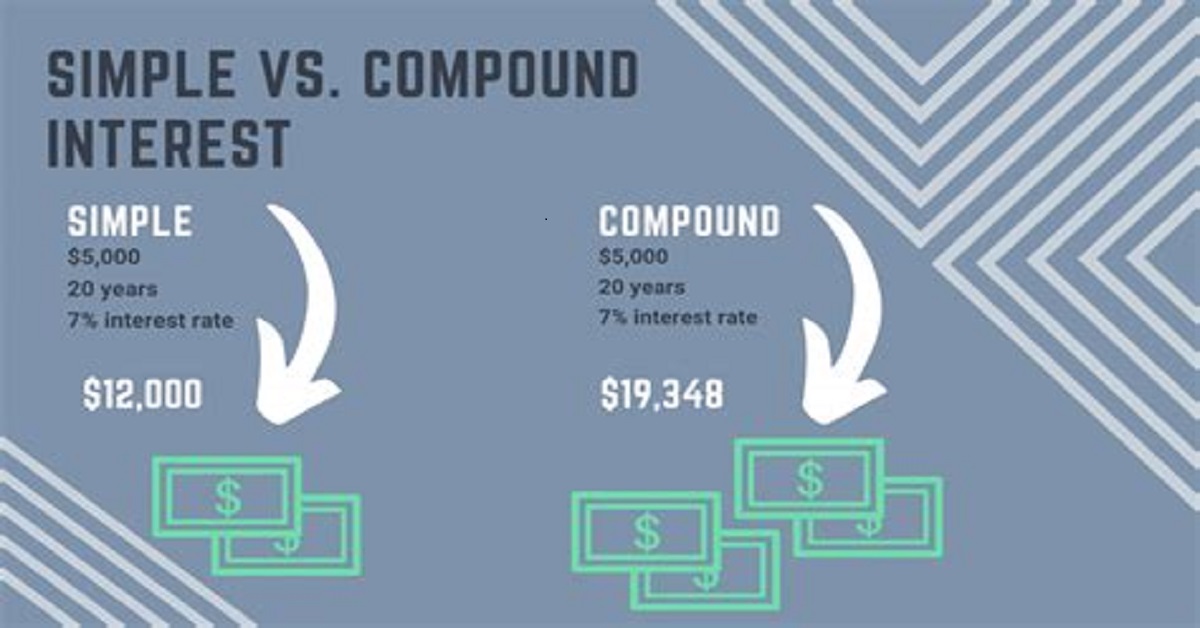
Understanding the difference between simple and compound interest is crucial in financial planning. While simple interest is calculated only on the principal amount, compound interest takes into account the interest that accumulates over time, leading to a significantly higher return on your investment if left to grow.
Many individuals think that all loans or savings will grow the same way if they have the same interest rate. But the way the interest is calculated is what really matters. The trick is compounding, which is a subtle but powerful process that can help your profits grow over time.
Calculate Simple Interest Instantly
Want to find out how much interest you’ll earn or pay using the simple interest formula? Try our free Simple Interest Calculator to get quick, accurate results. Whether you’re checking a short-term loan or a savings plan, this tool gives you clarity in seconds — no math required.
By reinvesting the interest earned, you create a snowball effect, where your earnings generate even more earnings. This principle not only applies to investments but also to debt, where compounding can work against you if not managed wisely.
In this Simple Interest vs. Compound Interest article, we’ll talk about simple and compound interest in plain English. We’ll also show you real-life instances and help you figure out when to use each type of loan, from short-term loans to long-term investments.
Let’s get started.
What is Simple Interest?
Let’s start with the basics. The easiest way to figure out interest is with simple interest, which is only charged or earned on the amount you started with. Nothing else.
Formula
Simple Interest (I) = Principal (P) × Rate (r) × Time (t)
If you put ₹5,000 into an account that pays 8% simple interest for three years,
I = 5,000 × 0.08 × 3 = ₹1,200
You will make ₹400 a year, which adds up to ₹1,200 after three years. Your final amount is ₹6,200.
That’s it—no “interest on interest.”
In the Real World
When you borrow or lend money for a short time, simple interest is common. This method is used for things like car loans, quick personal loans, and some government bonds. It is easy to understand, clear, and predictable.
You lend someone ₹1,00,000 for a year at 10% interest. You already know you’ll make ₹10,000, so there are no surprises or small print. That’s why many borrowers like simple interest: it’s fair and easy to understand.
How to Use?
Simple interest keeps things simple if you own a small business or lend money to someone privately. You know exactly how much you’ll get back, and there won’t be any extra confusion. It’s also best when the loan or deposit period is short, usually less than a year.
What does “compound interest” mean?
Let’s discuss one of the most powerful concepts in finance: compound interest. This phenomenon occurs when your interest begins to earn interest, causing your investment to grow at an accelerating rate over time. It can turn a modest initial investment into a substantial sum over the years, making it a vital principle for anyone aiming to build wealth. By leveraging the power of compound interest, individuals can significantly enhance their savings and achieve their financial goals more effectively.
Formula
A = P × (1 + r/n)^(n × t)
Where:
t = Years of time
A = Final amount (principal plus interest)
P = the main amount
r = the rate of interest per year
n = Number of times the interest is added to the principal each year
For Example
If you put ₹5,000 into an account with 8% interest that compounds every year for three years,
A = 5,000 × (1 + 0.08)^3 = ₹6,299.47
Interest earned = ₹6,299.47 – ₹5,000 = ₹1,299.47
That’s ₹99 more than simple interest over the same time period. At first, that’s not a big difference, but it gets much bigger over the years.
In the Real World
You can find compound interest in your bank’s fixed deposits, SIPs, credit card balances, and mutual funds.
Compound interest is what makes people rich, but it can also lead to debt. The same factor that contributes to the growth of your savings can also increase your unpaid credit card bills.
To harness the power of compound interest effectively, it’s crucial to manage your debts wisely and invest strategically. By prioritizing savings and minimizing high-interest liabilities, you can maximize the benefits of compounding over time.
That’s why Albert Einstein is said to have called it the “eighth wonder of the world.” “He who understands it, earns it; he who doesn’t, pays it.”
How to Use
Long-term thinkers benefit from compound interest. Compounding can turn small, regular savings into a large amount if you are saving for a goal, like buying a house, paying for school, or saving for retirement.
By starting early and being consistent, individuals can take advantage of the exponential growth that comes with time. This approach not only enhances financial security but also fosters a mindset geared towards patience and strategic planning.
Over 20 to 30 years, even a 1% difference in the rate or compounding frequency can add lakhs.
A small example that shows a big truth about money
Let’s do it.
Ravi and Meena both placed ₹20,000 into an account that pays 7% interest for 10 years. Ravi choose simple interest, whereas Meena picks compound interest.
Ravi’s simple interest is ₹20,000 plus (20,000 × 0.07 × 10), which is ₹34,000.
Meena’s compound interest is ₹20,000 times (1 + 0.07)^10, which equals ₹39,343.
Meena gets ₹5,343 more at the end of ten years because her interest was stacking up.
If you spread it out over 20 or 30 years, the difference may pay for a vacation, a gadget, or perhaps part of your retirement savings. That’s the beauty of compounding that happens quietly.
Simple Interest vs Compound Interest: Side-by-Side

| Feature | Simple Interest | Compound Interest |
|---|---|---|
| Interest base | Principal only | Principal + accumulated interest |
| Growth pattern | Linear | Exponential |
| Returns over time | Modest | Larger over long term |
| Complexity | Simple to calculate | More complex (depends on compounding frequency) |
| Best use | Short-term loans, clarity | Long-term investing, reinvestment |
| Risk in debt | Safer for borrower | Can escalate debt rapidly |
This table helps you instantly see how Simple Interest vs Compound Interest differ.
How Changing the Frequency of Compounding Affects Returns
How often interest compounds is a big difference between simple interest and compound interest.
- Once a year, every year
- Twice a year: semi-annually
- Four times a year is quarterly.
- Monthly or daily: growth even faster
₹5,000 at 8% for three years is an example.
- ₹6,299 a year
- Compounding every three months: ₹6,320
- ₹6,326 every month
More frequent compounding means faster growth.
The Rule of 72: A Quick Way to Figure It Out
The Rule of 72 is another common topic in the Simple Interest vs Compound Interest debate. It is a quick way to figure out how long it will take for your money to double.
Years to double = 72 Annual Interest Rate (%) Years to double ≈ 72 {Annual Interest Rate (%) Years to double = Annual Interest Rate (%)72
Your money will double in about 12 years if you pay 6% interest. It doubles in about eight years at 9%.
This rule of thumb provides a straightforward method for estimating the time needed for an investment to grow significantly. Understanding this concept can help individuals make more informed decisions about their savings and investment strategies.
This rule only works for compound interest, not simple interest. However, it does give you a quick idea of how long-term growth works.
Situations in Real Life
Scenario 1: Car Loan (Simple Interest)
Loan: 5 years at 7% simple interest on ₹2,00,000
- Interest = 2,00,000 × 0.07 × 5 = 70,000
- Total amount to be paid back: ₹2,70,000
Scenario 2: Putting money into something (compound interest)
Putting ₹50,000 into an investment at 8% for 10 years (compounded once a year)
- Simple Interest = ₹40,000 (Total = ₹90,000)
- The total amount is ₹1,07,946, and the compound interest is ₹57,946.
This clearly shows that compound interest makes your savings grow faster than simple interest.
Scenario 3: Putting money into something over time
You put ₹50,000 into an account that earns 8% interest that compounds every year for 10 years:
- The result of simple interest is ₹90,000 (₹40,000 in interest).
- The result of compound interest is about ₹1,07,946, with about ₹57,946 in interest.
Scenario 4: Long-term horizon (20 or 30 years)

Let’s see a table showing growth under both methods (8% annual) with ₹50,000 principal:
| Years | Simple Interest (Total) | Compound Interest (Final) |
|---|---|---|
| 5 | ₹70,000 + principal = ₹1,20,000 | ~₹73,466 + principal = ~₹1,23,466 |
| 10 | ₹40,000 + principal = ₹90,000 | ~₹1,07,946 total (principal + interest) |
| 20 | ₹80,000 + principal = ₹1,30,000 | ~₹2,33,000+ (because of compounding) |
You see compound interest’s advantage grows over time.
Continuous Compounding
There is also the idea of continuous compounding, which means that interest compounds at every possible moment. This can help you understand the difference between simple interest and compound interest even better.
In math, A = P ertA = P \, e^{r t}A=Pert
The number eee is a mathematical constant that is about 2.71828. This is the highest possible frequency of compounding.
Continuous compounding is more of a theoretical or advanced finance concept, but it helps you understand how much compounding can do.
The risks of compound interest when you’re in debt
Every kind of power has a bad side. Compound interest can help your investments grow, but it can also ruin you when you use it to pay off debt.
- Credit cards often use compound interest, which means that unpaid balances earn interest on top of interest.
- If you miss payments on a mortgage with interest that compounds monthly, it could take you longer to pay it off.
- Negative amortization means that paying only part of the interest makes the debt bigger instead of smaller.
Knowing the difference between simple and compound interest can help you avoid risky debt traps.
Inflation and Real Returns
Inflation is something that a lot of “interest” articles leave out. Even if your money grows through compound interest, your real buying power may not.
- Let’s say your nominal return is 8% and inflation is 4%. Your real return is about 4%.
- You want compound interest that beats inflation for long-term investments.
- When comparing simple interest to compound interest, growth is important. Inflation, on the other hand, eats away at value, so always look at returns in “real” terms.
Tools for figuring out and comparing
When you try formulas by hand, you make mistakes. These tools are useful:
- EMI Calculator: Find out how much of your loan payment goes to interest and how much goes to the principal.
- SIP Calculator: see how your regular investments will grow over time.
- Age Calculator: Find out how many years you have left to let compound interest work for you.
You can quickly test “what-if” scenarios with tools.
When to Use Simple or Compound Interest
When to use Simple Interest:
- You get loans for a short time.
- You want payments that are easy to plan.
- You like clear pricing structures.
When to Use Compound Interest:
- You put money into things for a long time.
- You’re putting money away for school or retirement.
- You want your money to grow over time.
Knowing the difference between simple interest and compound interest can help you make better decisions about borrowing and investing.
How to Calculate Interest Easily
Instead of using manual formulas, you can calculate both simple and compound interest in seconds using our free tools:
- EMI Calculator – to plan loan repayments.
- SIP Calculator – to see how compounding grows investments.
- Age Calculator – to plan how early to start investing for maximum benefit.
These calculators save time and show real-world results instantly.
Benefits of Understanding Interest Types
Knowing the difference between Simple Interest vs Compound Interest helps you:
- Choose smarter investment options.
- Avoid debt traps.
- Plan long-term wealth growth.
- Understand your financial statements.
- Make informed decisions about FDs, SIPs, or loans.
Final Thoughts
In conclusion, Simple Interest vs Compound Interest may sound like academic jargon, but they have a real and strong effect:
- Simple interest exhibits a linear growth pattern, offers predictability, and is typically more advantageous for borrowers.
- Compound interest: growth that gets bigger and bigger, excellent for building wealth over time (but risky if you have debt).
- Understanding the differences between these two types of interest can significantly impact financial decisions. Whether you are saving for a future goal or managing existing debt, knowing how each interest type works allows you to make informed choices that align with your financial objectives.
You have a decent understanding if you add in things like the Rule of 72, continuous compounding, and how inflation affects things.
Before you pick a loan or investment, ask:
- Is the interest simple or complex?
- How often does it compound if it is?
- What is the real return after inflation?
- Use our tools to simulate: Age Calculator, EMI Calculator, SIP Calculator.
Mastering Simple Interest vs Compound Interest empowers you to make smarter financial decisions — whether saving, investing or borrowing.